Author
Cheolmin Kim, Ph.D candidate in Industrial Engineering and Management Sciences, Northwestern University
[email protected]
Principal Component Analysis (PCA) is one of the most popular dimensionality reduction techniques. Given a large set of possibly correlated features, it attempts to find a small set of features principal components that retain as much information as possible. To generate such new dimensions, it linearly transforms original features by multiplying loading vectors in a way that newly generated features are orthogonal and have the largest variances with respect to the L2-norm.
Although PCA has enjoyed great popularity, it still has some limitations. First, since it generates new dimensions through a linear combination of original features, it is not able to capture non-linear relationships between features. Second, as it uses the L2-norm for measuring variance, its solutions tend to be substantially affected by influential outliers. To overcome these limitations of PCA, we present L1-norm kernel PCA model that is robust to outliers as well as captures non-linear relationship between features.
Model and Algorithm
Let us denote the data vector by $\text{a}_i$, and the loading vector by $\text{x}$. Letting $\Phi$ be a possibly nonlinear mapping, L1-norm Kernel PCA is formulated as follows:
\begin{align}
& \text{maximize} && \sum_{i=1}^n |\Phi(\text{a}_i)^T\text{x}| \\
& \text{subject to} && \|\text{x}\|_2=1.
\end{align}
Finding the optimal solution for the above problem is not straight-forward since it is not only non-convex but also non-smooth. To develop an efficient algorithm, we first reformulate it to the following form:
\begin{align}
& \text{minimize} && \|\text{x}\|_2 \\
& \text{subject to} && \sum_{i=1}^n |\Phi(\text{a}_i)^T\text{x}|=1.
\end{align}
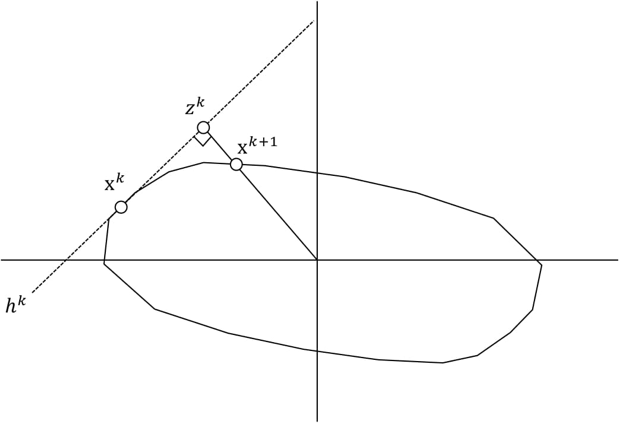
The reformulated problem is geometrically interpretable where the goal is to minimize the distance to the origin from the linear constraint involving the L1-norm terms. The main idea of the algorithm is to move along the boundary of the constraint so that the distance to the origin of the iterate decreases.
The above approach is also applicable to L2-norm PCA, and interestingly, the corresponding algorithm for L2-norm PCA is well-known Power iteration. Therefore, we can understand it as a counterpart of Power iteration to L1-norm PCA. Moreover, as in the case of L2-norm kernel PCA, the kernel trick is possible in the above algorithm making the computation of explicit mapping $\Phi$ unnecessary. While the above algorithm finds the leading loading vector, the remaining ones can be found by deflating the kernel matrix and recursively applying the same algorithm.
Convergence Analysis
We have the following results regarding the convergence of the algorithm.
- The algorithm terminates in a finite number of steps.
- $\|\text{x}^k\|-\|\text{x}^*\|$ where $\|\text{x}^*\|$ is the final iterate decreases at a geometric rate.
- By multiplying an appropriate scalar to the final iterate $\text{x}^*$, we can get a local optimal solution to L1-norm PCA.
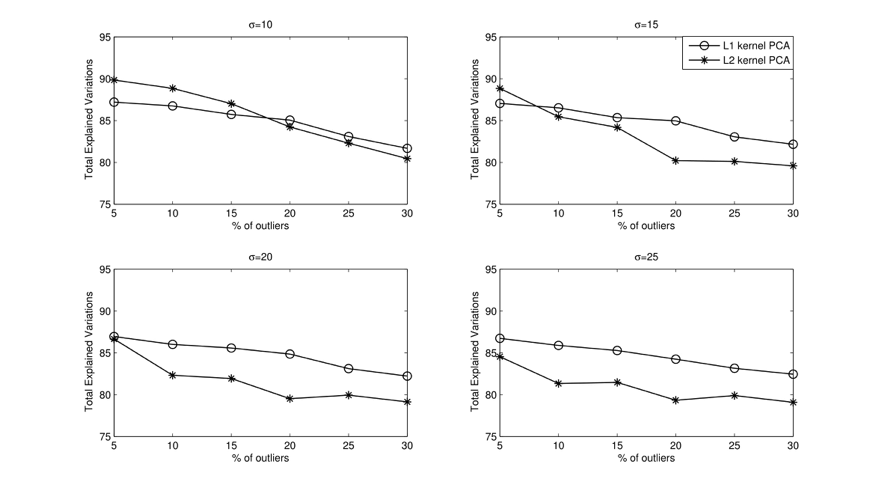
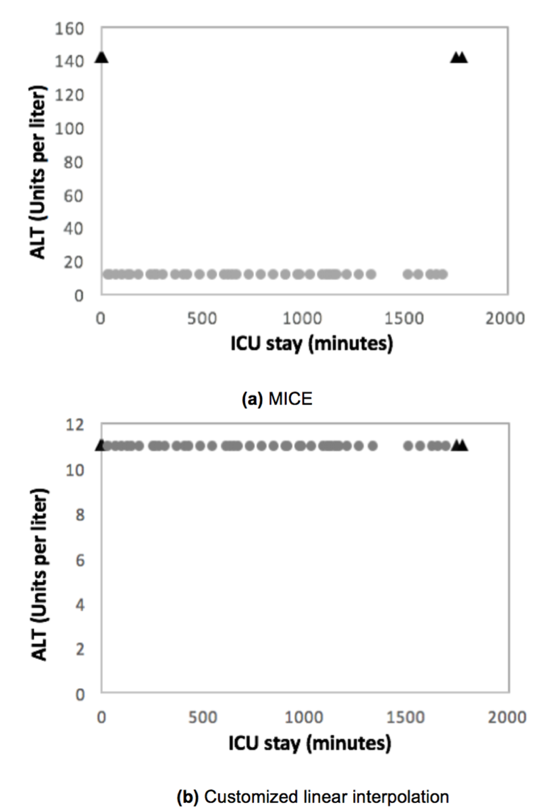
From the modeling perspective, L1-norm kernel PCA has an advantage over L2-norm kernel PCA in the presence of influential outliers. To show the robustness of L1-norm kernel PCA, we consider two data sets: One is original data whose covariance matrix has a low rank, and the other one is noisy data obtained by corrupting $r\%$ of observations in the original data. To measure the robustness, we compute how much variation of original data is explained by the loading vectors obtained by applying each kernel PCA algorithm on noisy data. The following figure shows the experimental results varying the width $\sigma$ of Gaussian kernel and the noisy level $r$. As shown in the figure, the loading vectors obtained by L1-norm kernel PCA from the noisy data better explain the variation of the original data.



 RSS Feed
RSS Feed